| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 유니티
- uclidean algorithm
- c#
- C
- 분할축 이론
- 백준
- 수학
- Graham Scan
- Vector
- Unity
- linux
- 내적
- SOH
- 리눅스
- dp
- 우분투
- 다이나믹 프로그래밍
- 문제풀이
- PS
- 보로노이다이어그램
- Doubly Connected Edge List
- 알고리즘
- 충돌 알고리즘
- GJK
- 외적
- Expanding Polytope Algorithm
- AABB
- C++
- ubuntu
- 벡터
- Today
- Total
마이 플밍 블로그
벡터 외적 본문
벡터의 외적은 간단히 말하면
다음과 같다.
두 벡터를 가지고 다른 벡터를 만드는 연산
이렇게 만들어진 벡터는 처음 주어진 두 벡터 모두에게 수직이 된다.
벡터의 외적은 수식으로 다음과 같이 표현된다.

내적에서는 * 로 연산을 표현하였지만 외적은 X를 쓰는 것에 주목하자
이렇게 외적으로 구한 벡터 a의 크기는 다음과 같이 구할 수 있다.
$$\left \| v \right \| = \left \| v \right \| \cdot \left \| w \right \| \cdot sin \theta$$
v = a w = b

내적 공식과 비슷해보이지만 cos가 아닌 sin을 사용한다.
외적 벡터의 크기는 두 피연산자 벡터들로 이루어지는 평행사변형의 넓이와 같음을 알 수 있다.
벡터의 외적은 각 벡터의 x,y,z 성분을 다음과 같이 연산하여 구할 수 있다.
$$v = (v_{x},v_{y}, v_{z}), w = (w_{x},w_{y}, w_{z})$$
$$v X w = (v_{y}\cdot w_{z} - w_{y}\cdot v_{z},v_{z}\cdot w_{x}-w_{z}\cdot v_{x},v_{x}\cdot w_{y}-w_{x}\cdot v_{y})$$
외적의 수식 자체를 외울 필요는 없으니 총 9번의 연산이 필요하다는 것은 알아두자. 내적의 경우 교환 법칙이 자연스럽게 적용되나 외적은 그렇지 않다. 외적은 곱하는 순서에 따라서 결과 벡터의 방향이 반대로 바뀌기 때문이다.

3차원 좌표계는 크게 오른손 좌표계와 왼손 좌표계로 나누어지는데, 보통 수학에서는 오른손 좌표계를 표준으로 쓰지만 3D 그래픽 라이브러리에 따라서는 왼손 좌표게를 쓰는 경우로 있다.
대표적인 경우가 DirectX, RenderMan 등이다. 반대로 오른손 좌표계는 OpenGL, XNA이 있다.
외적 결과 벡터의 방향을 알려면 오른손 좌표계는 오른손 왼손 좌표계는 왼손을 사용해야 한다.
엄지를 세우고 나머지 손가락들을 접었을 때 외적 수식에 나오는 차례대로 피연산자 벡터들을 만나게 하자.
그러면 엄지의 방향이 결과 벡터의 방향과 동일하다.

그림과 같이 벡터A와 B가 있고 서로 외적을 하는 순서에 따라 결과가 달라지는 것을 알 수 있다.
외적의 활용도는 어디에 있을까? 가장 흔한 예로는 평면의 법선 벡터를(normal vector)를 구할 때이다.
일반적으로 3차원에서 평면을 표현할 때 평면상의 한 점과 평면과 수직인 벡터를 사용한다. 이 벡터를 평면의 법선 벡터라고 한다. 평면의 세 점이 주어질 경우 다음과 같이 외적을 이용해서 평면의 법선 벡터를 구할 수 있다.


u가 이 평면의 법선 벡터가 된다
다른 예로는 두 벡터의 평행 여부를 판단할 때이다.
이미 벡터의 내적을 이용해서 두 벡터가 평행한지 판단할 수 있었지만 만약 두 벡터가 단위 벡터가 아니라면 정규화를 해야하 하는 부담이 있다. 이럴 때는 외적을 사용하는 것이 더 효과적이다. 두 벡터가 서로 평행하다면 두 벡터의 외적으로 나온 벡터의 크기는 0이 되는것을 이용한다.
이는 두 벡터가 평행이면 그 사이각이 0도 이거나 180도 이어야 하며, 이때 사이각의 sin 값은 0이된다는 사실에서 알 수 있다.
즉 외적 벡터의 크기를 구하는 수식에서 사이각의 sin 값이 곱해지기 때문에 평행한 두 벡터의 외적은 영 벡터를 산출함을 알 수 있다. 또한, 벡터의 크기의 제곱은 자기 자신과의 내적과 같다는 것을 말하였다.
다음과 같이 평행성 여부를 판별할 수 있다.
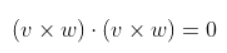
이러면 벡터들을 정규화 하지 않아도 되어 14번의 연산(1번의 외적과 내적)이면 결과를 알 수 있다.
정규화와 내적으로 23번의 연산이 필요했던 것과 비교하면 낫다.
또다른 예로는 카메라 행렬을 구할 때이다.
카메라 행렬을 구하기 위해서는 카메라를 원점으로하고 카메라가 보는 방향 벡터와 게임 세계에서 천장이나 하늘을 가리키는 상향(up) 벡터를 가지고 카메라 좌표계를 만들어야 한다. 이 두 벡터를 가지고 두 번의 외적을 통해서 카메라 좌표계의 세 축을 구할 수 있다.
주인공 A와 적 B가 있을 경우 적이 주인공의 오른쪽에 있는지 왼쪽에 있는지 알고 싶다고 하자, 이때 주인공 A의 전방 벡터를 v 주인공 A에서 적 B를 향하는 벡터를 w 게임 세계의 상향 벡터를 up이라고 하면 다음과 같은 판별식을 만들 수 있다.
만약 up*(v X w) > 0이면 적 B는 A의 왼쪽
up*(v X w) < 0 이면 오른쪽

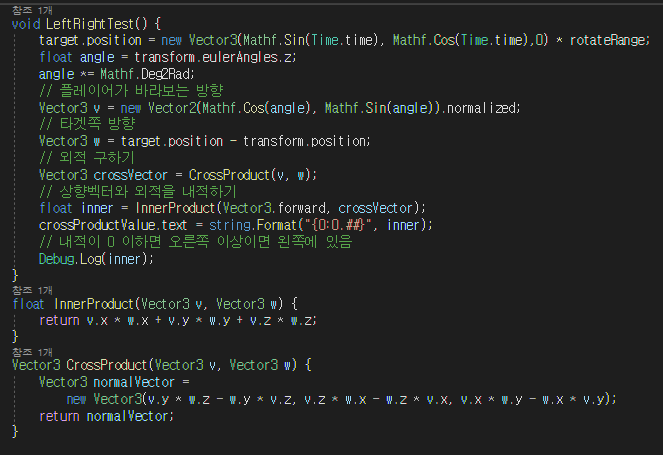
만약 B가 A의 왼쪽에 있다면 법선 벡터는 위쪽으로 향할 것이고 오른쪽에 있다면 아래쪽 방향으로 생길것이다.
이상태에서 상향 벡터와 내적을 한다면 그 값은 왼쪽에 있으면 양수 오른쪽은 음수가 나오게 될것이다.


