| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Doubly Connected Edge List
- Unity
- GJK
- 분할축 이론
- Graham Scan
- linux
- 충돌 알고리즘
- C++
- c#
- 다이나믹 프로그래밍
- 내적
- 외적
- ubuntu
- uclidean algorithm
- 보로노이다이어그램
- dp
- 리눅스
- 벡터
- 유니티
- Vector
- 수학
- PS
- 문제풀이
- 알고리즘
- 우분투
- C
- SOH
- AABB
- Expanding Polytope Algorithm
- 백준
- Today
- Total
마이 플밍 블로그
GJK-EPA 알고리즘 본문
아래 링크는 GJK 알고리즘에 대한 설명이다.
GJK 알고리즘을 잘 모르면 읽어보길 바란다.
충돌 알고리즘(collision detection algorithms)
충돌 알고리즘인 AABB, OBB, GJK 알고리즘에 대한 설명
www.slideshare.net
EPA(Expanding Polytope Algorithm)의 필요성
GJK 알고리즘으로 우린 도형이 충돌판정을 알 수 있다. 하지만 말그대로 충돌을 했냐 안했냐만 알 수 있기 때문에 이것만 가지고선 제대로된 게임을 만들 수 없다. 그래서 우린 EPA를 통해서 충돌한 Edge 방향을 가리키는 노멀인 Contact Normal과 얼마나 깊게 충돌했는지 알수 있는 충돌 깊이 값인 Depth를 알아내어야 한다.
GJK에서는 민코스키 차가 원점을 포함하면 충돌이 되었다고 했는데 민코스키 차에서 가장 가까운 점에서 원점으로 가는 걸가 충돌 깊이다.
EPA 동작 원리
1. GJK에서 사용한 Simplex를 Polytope로 지정한다.
2. 원점과 Polytope의 Edge의 거리가 가장 가까운 Edge를 고른다.
3. 원점에서 가장 가까운 Edge 쪽을 가리키는 Vector를 이용해 Support Point를 구하고 Edge의 두 점 사이에 Support를 삽입해서 Polytope를 확장한다.
4. Support Point가 Polytope에 포함되 있으면 확장을 중단한다.
5. 이렇게 최종적으로 완성된 Polytope의 Edge중 가장 가까운 Edge와의 거리가 Depth, 원점에서 Edge 쪽 방향이 Contact normal이 된다.
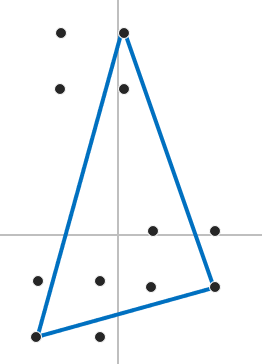
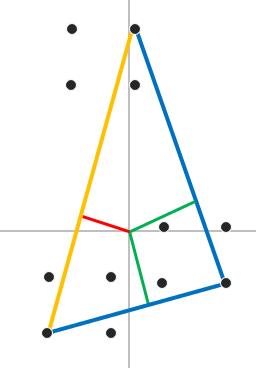
첫번째로 GJK알고리즘에서 쓴 Simplex를 Polytope로 사용했을 때이다.
왼쪽 그림이 Polytope의 본모습이고 오른쪽은 원점과 Polytope의 Edge들간의 거리를 비교했을 때의 그림이다. 빨간선이 Edge와 원점의 최소거리이고 주황 선이 원점과 가장 가까운 Edge이다.
빨간 선 즉 원점에서 부터 주황선쪽으로 가는 곳에 있는 가장 멀리 있는 Support Point를 구해서 확장을 해야한다.
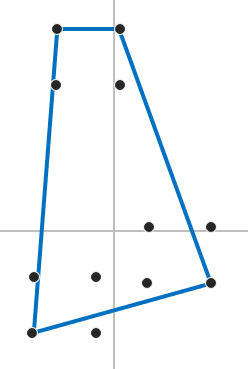
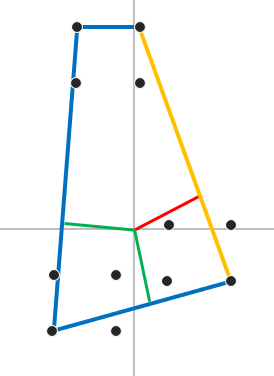
확장을 하면 위와같이 변하고 확장을 한번 더 한다.

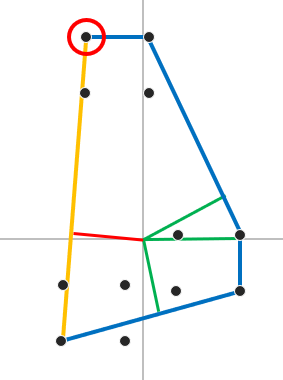
그리고 왼쪽에서 한번더 확장 할려고 하면 오른쪽 같이 되는데 다음 Support Point가 Polytope에 포함되 있는것이면 확장을 중단한다.
주요코드들
가장 가까운 Edge찾기
static Edge FindClosestEdge(List<Vector2> s) {
Edge closest = new Edge();
closest.distance = float.MaxValue;
// polytope 정점 순회
for (int i = 0; i < s.Count; ++i) {
int j = i + 1 == s.Count ? 0 : i + 1;
Vector2 a = s[i];
Vector2 b = s[j];
Vector2 ab = b - a;
Vector2 oa = a;
// polytope의 모서리 벡터의 노멀벡터 구하기
// 아래걸로 하나 위에걸로 하나 상관없음
//Vector2 n = new Vector2(e.y, -e.x).normalized;
Vector2 n = Vector3.Cross(Vector3.Cross(ab, oa), ab);
n.Normalize();
// n의 방향이 원점에서 Edge쪽 방향을 바라보도록 조정
// 만약 n과 a의 사이각이 90도 이상일경우
if (Vector2.Dot(n, a) < 0) {
n = -n;
}
// normal 벡터인 n과 a를 내적함으로써 원점에서 Edge의 거리를 구함
float d = Vector2.Dot(n, a);
if (d < closest.distance) {
closest.distance = d;
closest.normal = n;
closest.index = j;
}
}
return closest;
}
EPA 수행
public static Vector2 epa(List<Vector2> polytope, Polygon shapeA, Polygon shapeB) {
// 민코스키 차 포인트들
HashSet<Vector2> minkowskiDPoints = new HashSet<Vector2>();
List<Vector2> shapeAPoints = shapeA.GetRotatePoints();
List<Vector2> shapeBPoints = shapeB.GetRotatePoints();
// 모든 민코스키 차 정점들 추가하기
for (int i =0; i < shapeAPoints.Count; i++) {
for (int k = 0; k < shapeBPoints.Count; k++) {
minkowskiDPoints.Add(shapeAPoints[i] - shapeBPoints[k]);
}
}
List<Vector2> minkowskiDifPoints = new List<Vector2>(minkowskiDPoints);
Edge edge;
int safe = 0;
while (safe < 1000) {
edge = FindClosestEdge(polytope);
Vector2 support = SupportPoint(minkowskiDifPoints, edge.normal);
if (polytope.Contains(support))
break;
// Polytope 확장
polytope.Insert(edge.index, support);
safe++;
}
edge = FindClosestEdge(polytope);
if (safe == 1000)
Debug.Log("세이프");
return edge.normal * (edge.distance + 0.001f);
}
