| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- GJK
- 충돌 알고리즘
- Doubly Connected Edge List
- c#
- 다이나믹 프로그래밍
- 분할축 이론
- AABB
- uclidean algorithm
- Graham Scan
- 내적
- linux
- 벡터
- 리눅스
- PS
- Unity
- ubuntu
- 알고리즘
- Expanding Polytope Algorithm
- C++
- Vector
- 외적
- 문제풀이
- 보로노이다이어그램
- 우분투
- 백준
- dp
- 유니티
- C
- SOH
- 수학
- Today
- Total
마이 플밍 블로그
Doubly Connected Edge List(DCEL) 본문
DCEL 이중 연결 가장자리 목록 혹은 half-edge data structure 라고도 불리는 이것은
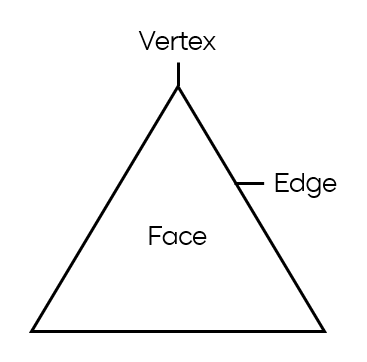
일반적으로 위처럼 폴리곤이 Face Vertex Edge 3개의 요소로 이루어지는 구조를 뜻하는데 각 요소의 뜻은 다음과 같다.
Face - 폴리곤의 내부
Vertex - 폴리곤의 정점
Edge - 폴리곤의 가장자리

DCEL은 위와같은 모습이 되는데 한 폴리곤의 내부가 시계방향 혹은 반시계방향으로 정렬되 있는데 만약 모서리가 면의 경계에 있다면 그 위치에 있는 모서리는 두개이고 각 모서리를 가진 폴리곤의 회전 방향은 정 반대이다.
방향만 다른 같은 모서리가 두개있는 것이 마치 한 모서리를 반으로 가른것 같아서 half-Edge라고도 불리는 것 같다.
폴리곤을 이루는 각 요소는 다음과 같은 데이터를 가지고 있는데
Face - 폴리곤을 이루는 한 Edge
Vertex - 자신이 포함된 폴리곤의 Face
Edge - p1Vertex, p2Vertex, prevEdge, nextEdge, oppositeEdge
Face1의 경우 E1, E2, E3중에 하나를 가지게 되고
Vertex1은 E2를 가지게 되고
Edge1은 p1으로 V3 p2로 V1 prevEdge는 E3 nextEdge는 E2 oppositeEdge는 E4가 된다.
DCEL은 도형 기하학에서 쓰이기 좋은데 예를 들어 한 메쉬가 있다고 가정했을 때 메쉬의 한 triangle를 구하려고하면 하나하나 일일이 찾는 브루트 포스 방식이 아니라 DCEL 폴리곤 데이터를 이용해 원하는 triangle을 찾아간다면 찾는데 걸리는 시간이 획기적으로 줄어들 수 있다.
DCEL를 사용하는 대표적인 예시중 하나가 보로노이 다이어그램인데
아래쪽 링크를 타고들어가서 확인해 보면 좋을거 같다
Use math to solve problems in Unity with C# - Voronoi Diagram | Habrador
참고자료
https://www.ics.uci.edu/~goodrich/teach/geom/notes/DCEL.pdf
